Depthwise Separable Convolutions
what do they do?
Regular Convolution
A normal convolution is like a linear layer inside a neural network, except that it works on patches of the input instead of the taking the entire image into account, like a fully connected layer. The weights in a convolutional layer is made up of kernels. At the start of training these kernels are made up of random numbers, but after training allow the network to identify patterns that make it useful for image classification or object detection.
There are m kernels during a convolution. where m is the number of output channels. Each kernel has a width and height (like 3x3 or 5x5) and a number of channels, which is the same number of input channels. For example, with a 224x224 image with 3 channels (rgb), we could ‘convolve’ the image with 8 3x3 kernels, outputting a 222x222x8 feature map (in this case there is no padding, no dilation and the stride is just 1). A convolution multplies each number in it’s kernel by it’s corresponding place in the image, summing those multplications up, and then shifting the kernel over by one (or whatever the stride is), and repeating for the entire input.
The most common convolution you’ll see is the 3x3 convolution (VGG, Mobilenet, YOLO as examples). It reduces the amount of multiplications needed, with the same number of input/output channels. One 5x5 convolution will take in the same amount of the image as two 3x3 kernels done one after the other, but doing the two 3x3 convoltuions instead results in less multiplications. For example, in a 224x224x3 image, doing a 5x5 convolution with 16 output channels results in 220*220*3*5*5*16 = 580,800,000 multiplications, while two 3x3 convolutions with the same number of output channels results in (222*222*3*3*3*16)+(220*220*3*3*3*16) = 42,199,488 multiplications. The second layer using 3x3 convolutions however will effectively be able to see a 5x5 part of the oringal feature map.
I’ll use 3x3 convolutions as the example for the rest of the post, with no padding/dilation and the strides will be set to 1.
Groups
Groups are another argument on how to describe a convolution operation. You’ll see it in the PyTorch documentation for Conv2d. Having n groups means splitting the input channels into n pieces, and using n groups of kernels, where each group of kernels will only process its corresponding input channel group.
Depthwise Separable Convolution
It turns out we can reduce the amount of computation required in a convolution using depthwise separable convolutions, which takes groups to the extreme shown in the MobileNet paper.
I’ll use a regular convolution to illustrate why this reduces computational cost. If we have an input feature map of shape 28x28x8, and a convolutional layer of 3x3 convolutions with 16 output channels, we have to do 26*26*3*3*8*16 = 778,752 multiplications. We will get a 26x26x16 feature map as the output.
There are two steps to a depthwise separable convolution. First, we perform a depthwise convolution, and then a pointwise convolution, which will get us the same complexity in our neural net but reduce the number of calculations needed.
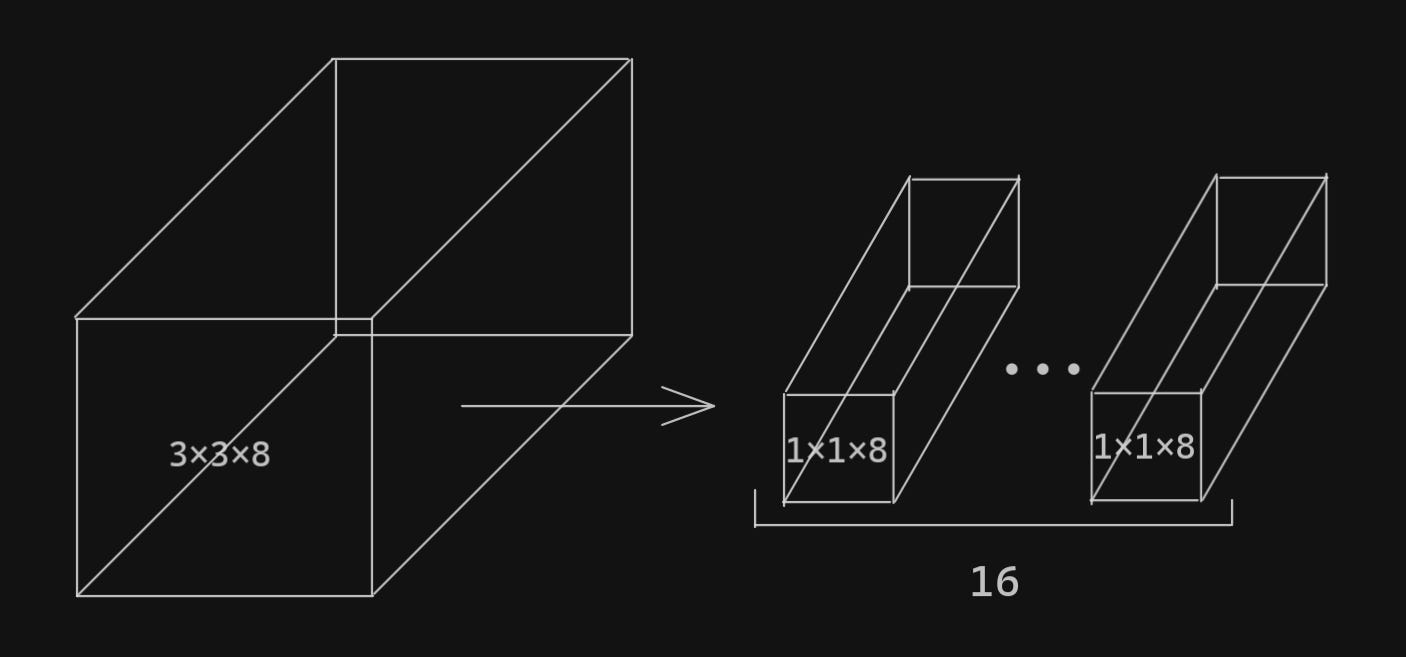
We seperate the incoming feature map into n groups, where n is the number of input channels. This means that each group will only have one channel. We can apply one 3x3 convolution to each group. This is the depthwise convolution. If we perform this for the same example, we will output a 26x26x8 feature map.
Next we will use 16 1x1 convolution kernels, which will be our pointwise convolution. This will output a 26x26x16 feature map, with exactly the same shape as doing a regular 3x3 convolution, each of the 16 kernels having 8 channels.
How does this improve performance? The depthwise convolution uses 26*26*3*3*8 = 48672 multiplications. The pointwise layer uses 26*26*8*16 = 86528 multiplications. In total 135200 multiplications, which is an 82% reduction in mulplications. The MobileNet paper shows that the reduction will be
where N is the number of kernels and D_K is the size of the kernels. Since most layers use 3x3 kernels, as you increase the number of output channels you approach 89% reduction in multiplications.
Conclusion
Using depthwise separable 3x3 convolutions massively reduces the amount of computation needed to perform these operations, while maintaining the same complexity in the neural network.